Python|탐색 알고리즘 뿌시기 (1) DFS, BFS 의 개념과 구현
#DFS #BFS #깊이우선탐색 #너비우선탐색 #탐색알고리즘 #알고리즘구현 #파이썬 #Python #탐색알고리즘 뿌시기
탐색 알고리즘과 자료구조, 직관적으로 이해하기
깊이 우선 탐색, 너비 우선 탐색 등,, 컴퓨터 공학을 전공하거나 개발을 공부하는 사람이라면 다들 한 번씩은 들어보고, 구현도 해봤을 대표적인 탐색 알고리즘입니다. 거기에 하나쯤 더한다면 효율을 생각한 A* (A star) 알고리즘 정도까지 있겠죠!
들어보긴 많이 들어봤는데, 그 개념과 구현은 생각보다 쉽지만은 않습니다. 이들을 탐색할 때 쓰이는 트리와 스택, 또는 큐 같은 자료구조까지, 알아야 할 것들이 너무 많기도 하구요! 저 또한 이 알고리즘들을 처음 접했을 때는 도대체 stack이 왜 필요하고, 넣었다 뺐다를 왜 하는 건지 잘 와 닿지 않았습니다.

사실은 이렇게 생긴 트리라는 게 어디에 쓰이는 무엇인지, 그리고 트리에서 탐색을 한다는 것 자체가 무슨 의미가 있는 것인지를 알지 못하고 알고리즘을 배우려고 했기 때문인 것 같기도 합니다.
그래서, 재미도 없고 와 닿지도 않는 트리에서의 탐색보다도, 일단 탐색이라는 게 도대체 뭔지를 직관적으로 먼저 이해해보려고 합니다!
탐색은 도대체 무엇이며, 왜 하는 걸까요?
자료 탐색이란, 아주 방대한 자료들이 쌓여 있을 때 우리가 원하는 자료를 찾는 작업을 말합니다. 예를 들어 데이터가 아주 많은 고객 데이터베이스에서 원하는 유저의 정보를 찾아 보여주고 싶을 때도 쓰이고, 구글에서 검색어를 쳤을 때 구글 데이터베이스에 쌓여있는 모든 관련 링크 또는 자료 중 관련된 것들을 찾아서 보여줄 때도 쓰이죠.
그냥 찾으면 되는 거지, 거기에 알고리즘이 대체 왜 필요해..! 라고 생각하실 수도 있지만, 도서관을 생각해보세요! 그 산더미같은 책 무덤에서 우리가 원하는 책 한 권을 잘 찾으려면 잘 짜인 정리체계가 필요하다는 것을 생각하면 조금은 와 닿을까요?

이렇게 모든 책들이 카테고리별로 잘 분류되어 있고, 그 안에서도 ㄱㄴㄷ 순으로 잘 정리되어 있다면 (-이렇게 분류하고 정리하는 작업은 "정렬 알고리즘"으로 처리되겠죠!) , 우리는 원하는 책을 찾기 위해 할 일은 단순히 어떤 카테고리인지 확인한 후, 그 안에서 ㄱㄴㄷ 순으로 책을 찾아나가는 것입니다. 이 모든 과정이 바로 탐색 알고리즘의 과정인거죠!
하지만 만약 책을 저렇게 잘 분류 해놓지 않는 도서관이라면 얘기가 달라집니다. 우리가 모든 책들을 하나하나 직접 확인하면서 원하는 책이 맞는지 아닌지 하루종일 도서관 안을 누벼야 하죠.. 😱
이렇게 가장 무식하고 원초적인 방법이 바로! 깊이 우선 탐색과 너비 우선 탐색 입니다.
두 탐색 알고리즘은 탐색을 어떤 순서로 하느냐만 살짝 다를 뿐, 어떤 효율성도 생각하지 않고 모든 자료를 하나하나 다 확인해 본다는 점은 똑같습니다. 우리가 탐색 알고리즘을 배울 때 가장 기본 알고리즘으로 제일 먼저 배우지만, 현실에서는 절대 쓰이지 않는 이유도 여기에 있죠.
바로, 너무 무식해서..!!!
인간은 시간과 자원을 (너무나) 아끼고 싶어하기 때문에 실제로 자료를 탐색해야 할 때는 절대 모든 것들을 하나하나 탐색하지 않습니다. 조금 더 빨리 탐색할 수 있는 방법이 꾸준히 제안되며 훨씬 효율적인 알고리즘들이 많이 개발되었는데, 먼저 DFS와 BFS를 알아본 후 다음 포스팅에서 더 발전된 알고리즘 중 비교적 간단한 A* 알고리즘까지 알아보고 구현해 보겠습니다!
탐색이 필요한 또 다른 세계, Game
자료 탐색에 대해 길게 설명했는데, 사실 탐색 알고리즘은 꼭 자료를 찾는 것이 아닌 상황에서도 요긴하게 쓰일 때가 많습니다. 그중 하나가 바로 게임이죠!
바둑 하는 인공지능, 알파고를 기억하시나요? 1996년, 체스가 인공지능에게 정복 된 이후로도 꽤 오랫동안 바둑은 절대 넘지 못할 산으로 여겨졌습니다. 바로 체스를 훨씬 능가하는 경우의 수 때문이었죠. 일단 8 x 8 로 총 64칸에서 이루어지는 체스판 개수로만 비교해도 바둑은 19 x 19 로 361개의 점이 있으니 큰 차이가 나고.. 모든 경우의 수를 다 계산하자면 어마어마하게 큰 숫자가 됩니다.
이렇게 엄청난 알파고를 개발한 딥마인드 팀은 알파고에 쓰인 알고리즘 중 몬테카를로 트리 탐색 알고리즘 이 있다고 밝혔습니다.
뭔지는 몰라도, 여기에 "탐색 알고리즘"이 있네요! 알파고가 바둑을 할 때 탐색 알고리즘은 왜 필요한 걸까요?
바둑은 수읽기가 중요한 게임입니다. 내가 돌을 내려놓을 수 있는 곳, 그리고 상대가 내려놓을 법한 곳들을 더 많이, 더 먼 미래의 수들까지 예측할 수록 게임에서 유리해지죠. 물론 모든 수를 다 읽을 수 있다면 승률은 100%가 될 것입니다. (하지만, 바둑에서 나올 수 있는 모든 경우의 수는 우주의 원자 개수보다 많다고 알려져있죠 😂)
여기서 바로 탐색이 사용됩니다.
예를 들어 현재 200개의 점이 남았다면 그 중 한 점에 놓아보고, 그 다음 상대의 돌을 예측해보고, 별로라면 다시 다른 점에 놓아보고, ... 이렇게 여러가지로 진행될 수 있는 게임 과정을 머릿속 (또는 알파고라면 메모리) 에서 반복하면서 최적의 수를 찾기 위해 여러 경우의 수들을 "탐색" 하는거죠.

자료 탐색이 아닌 게임에서도 경우의 수들을 확인한 후 어떤 것이 최적인지 알아내기 위해 탐색이 쓰인다고 하니, 어떻게 쓰이는지 직접 확인해보지 않을 수 없겠죠! 다음 글에서는 탐색이 쓰일 수 있는 여러 게임 중 8-Puzzle 과 미로찾기 두 가지 간단한 문제의 알고리즘을 직접 구현하고 결과를 확인해 보겠습니다.


우리가 직접 경험한 탐색 알고리즘
그렇다면, 혹시 우리가 실생활에 탐색 알고리즘을 써 본 적은 없을까요? 좀 더 와 닿는 사례를 들어보죠!
바둑 또는 다른 게임을 하면서 여러가지 경우의 수가 존재할 때, 가장 좋은 선택을 하기 위해 모든 경우의 수들을 메모지에 적어본 경험이 있나요? 아니, 만약 머리가 좋은 사람이라면 여러가지 경우의 수들을 다 머릿속에 기억해 두면서 몇 수 앞을 따져본 적이 있을 수도 있구요!
그런 적이 있다면, (없더라도 같이 상상해봐요!) 혹시 그 경우의 수들을 좀 더 체계적으로 따져보기 위해 1) 한 단계를 진행할 때 가능한 경우의 수 를 전부 써보고, 각각에 대해서 또 2) 두 단계를 진행할 때 가능한 경우의 수 를 써보면서 따져본 적이 있나요? 마치 나무에서 가지가 자라듯이 엄청나게 다양한 경우의 수가 막 퍼져나가는 그 그림이요!
이런 그림을 그려본 경험이 있다면 당신은 이미 "탐색 알고리즘"을 직접 실행해 본 적이 있는 겁니다. (그런 경험이 없더라도 상상할 수 있다면 해본겁니다!)
탐색에 쓰인다는 트리도 활용하면서요! (저 그림 자체가 트리입니다!)
만약 아래 그림처럼 1) 한 단계 진행 시 가능한 경우의 수, 2) 두 단계 진행 시 가능한 경우의 수 와 같이 매 단계에서 가능한 경우의 수들을 모두 확인하며 탐색한다면 그것이 바로 너비 우선 탐색 입니다. 간단하죠?! 뒤에서 또 설명하겠지만, 너비 우선 탐색은 이렇게 트리를 넓히면서 탐색하는 알고리즘입니다.
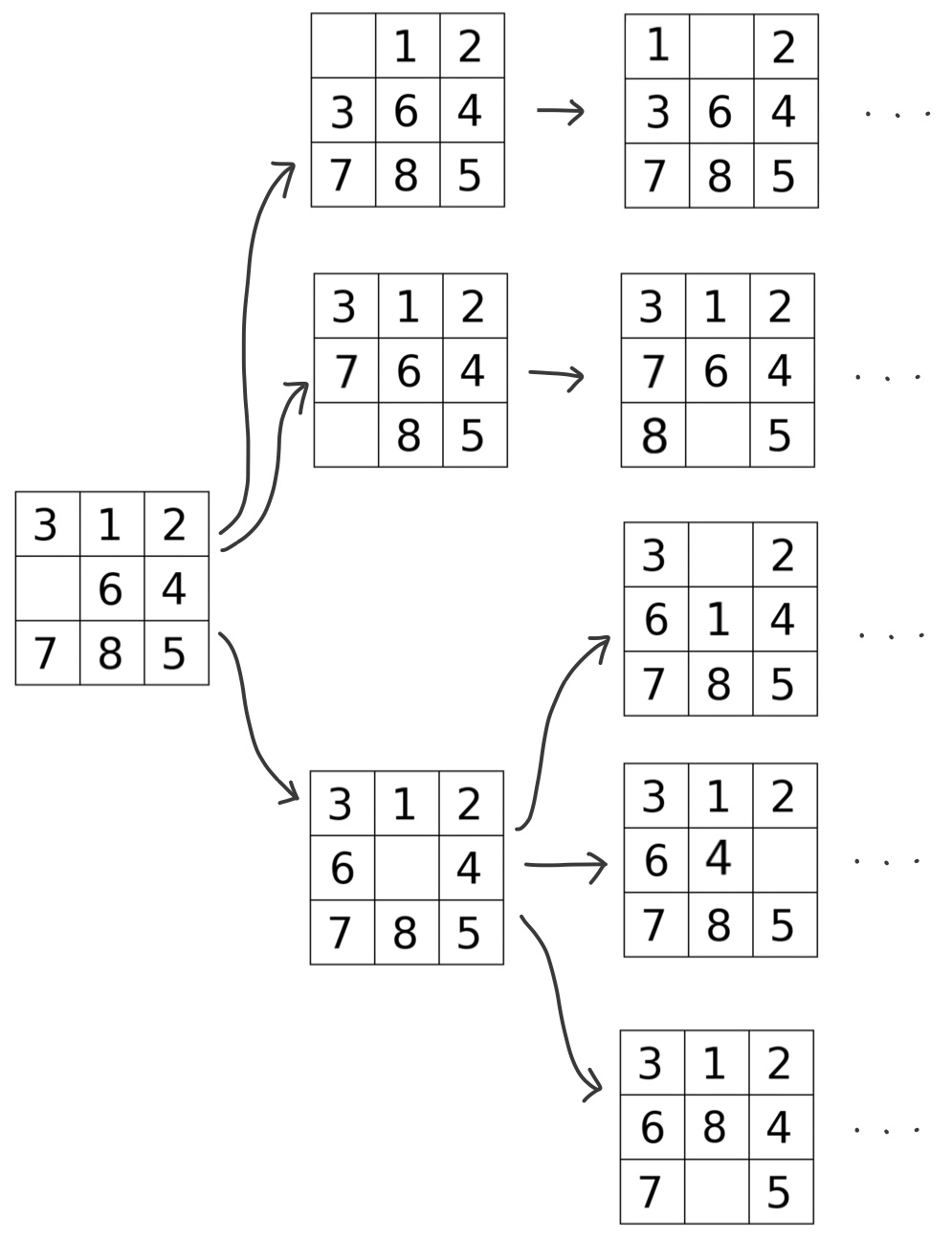
반면, 깊이 우선 탐색은 1) 여러 경우의 수 중 하나를 선택, 2) 선택 후 가능한 여러 경우의 수 중 또 하나를 선택 하는 식으로 매 단계에서 가능한 것 중 일단 하나를 선택해 끝을 볼 때까지 깊게 들어갑니다. 한 우물만 파서 끝에 도달했는데도 원하는 답이 안나왔다면, 그 직전으로 돌아왔다가 다시 또다른 끝을 확인합니다. 이러한 과정을 원하는 결과가 나올 때까지 반복하죠.

너비 우선 탐색과 깊이 우선 탐색이 어떤 건지 와 닿으시나요?
너비 우선은 매 단계에서 가능한 모든 경우의 수를 확인,
깊이 우선은 한 우물만 파고들며 끝을 볼 때까지 확인! 이라는 것만 이해하면 다 이해한 겁니다! 👍
그렇다면, 자료구조는 왜 필요한가
지금까지 모든 게 이해됐다면, 바로 알 수 있는 것이 한 가지 더 있습니다! 바로 스택/큐 같은 자료구조가 왜 필요한지 말이죠.
방금 이야기 했던 예시에서, 어떤 게임을 진행하면서 가능한 경우의 수들을 모두 생각해 보고, 그 이후의 경우의 수도 모두 확인해 볼 때 "메모지에 쓰면서" 또는 "머릿속에 기억해 두면서" 라는 표현을 사용했던 것, 기억하시나요? 우리가 직접 탐색할 때는 스택/큐 같은 자료구조를 명시적으로 쓰지는 않았지만 여전히 "메모지에 적어두기" 또는 "머릿속에 기억" 이라는 형태로 경우의 수들을 "저장" 해두었습니다.
특정 순간들의 상태를 저장해 두어야 그 다음 상태를 확인하면서 탐색을 이어나갈 수 있기 때문이죠!
만약 지금 시도해 볼 수 있는 경우의 수가 10가지일 때, 다른 9가지는 일단 잠시 두고 한 가지에 대해서 그 다음 단계를 생각해 본다면, 나머지 9가지는 어떻게 해야 할까요? 어딘가에 잘 저장해 두어야 지금 탐색할 선택지의 결말이 마음에 안 들었을 때 언제라도 다시 돌아와서 또 다른 선택지를 탐색해 볼 수 있을겁니다. 이렇게 "잠시 저장" 해 두는 과정은 프로그래밍으로 구현할 때도 당연히 필요합니다. 이를 위해 자료들을 담아둘 수 있도록 고안된 구조가 바로 스택 또는 큐입니다.
스택과 큐는 무엇이고, 어떻게 다른가
그렇다면, 깊이 우선 탐색에서는 스택이, 너비 우선 탐색에서는 큐가 필요하다고 하는데, 스택과 큐는 또 어떻게 다른 친구들일까요?
스택과 큐의 단어 뜻은 각각 "쌓는 것", 그리고 "줄을 서서 기다리는 것" 입니다. 둘 다 자료를 저장해 둔다는 성질은 같은데, 저장해 둔 자료를 사용하는 순서가 다릅니다.
스택은 말 그대로 "자료를 차곡차곡 쌓는 것"이기 때문에 박스 안에 쌓는 이미지를 생각해볼 수 있습니다.

위처럼 박스에 자료가 쌓인다면, 자료를 꺼낼 때는 어떨까요? 맨 마지막에 넣은 자료인 5번을 처음 꺼내야 그 밑의 자료를 꺼낼 수 있고, 그렇게 모든 자료들을 다 꺼내야 비로소 마지막에 처음으로 넣었던 자료인 1번을 꺼낼 수 있습니다. 이렇게 나중에(후) 넣은 것(입)을 먼저(선) 꺼낸다(출) 는 의미로, Last In, First Out (LIFO) 라고 표현합니다.
반면, 큐는 "줄을 서서 기다리는 것" 이라는 뜻을 가지고 있죠. 놀이기구 줄을 생각해 보면, 처음 줄을 선 사람은 먼저 타고, 나중에 줄을 선 사람은 나중에 탑니다. 즉, 줄에 합류 한 순서 그대로 줄을 빠져나가는 거죠. 비슷한 예로, 배드민턴 공 통을 생각할 수 있습니다. 배드민턴 공의 모양 때문에 오른쪽에서 공을 차곡차곡 넣으면 왼쪽부터 빼는 것이 편리하죠!

그래서 큐는 먼저(선) 넣은 것(입)을 먼저(선) 꺼낸다(출) 의 의미로 First In, First Out (FIFO) 라고 표현합니다.
이렇게 같은 용도이지만 다른 사용방식을 가진 스택과 큐를 탐색하면서 적절히 활용해 필요한 것들을 잠시 저장해 두거나, 필요할 때 다시 빼서 사용할 수 있습니다.
그렇다면 이제 탐색에 대한 모든 것을 이해했으니, 코드로는 어떻게 구현 되는지, 그리고 깊이 우선 탐색과 너비 우선 탐색에서 왜 각각 스택/큐를 사용해야 하는지 등 세부적인 것들을 진짜 코드로 확인하러 가보시죠!
깊이우선탐색 (DFS), 너비우선탐색 (BFS) 구현하기
지금까지 탐색 알고리즘과 그에 쓰이는 자료구조들을 모두 알아봤죠. 이제 DFS, BFS 알고리즘의 기본 형태를 파이썬 코드로 구현해 볼 것입니다.
기본 형태 구현은 말 그대로 뼈대를 잡는 과정으로, 어떤 문제를 푸느냐에 따라 다양하게 응용 또는 수정될 수 있습니다. 기본 형태를 완벽하게 이해한다면 어떤 문제에 적용시키더라도 어렵지 않게 내 입맛에 맞게 수정해서 사용할 수 있습니다!
DFS와 BFS의 탐색 과정을 직접 하나하나 확인하기 위해 아래와 같은 간단한 트리 형태를 하나 정해두고, 탐색 순서를 하나씩 확인해보겠습니다.
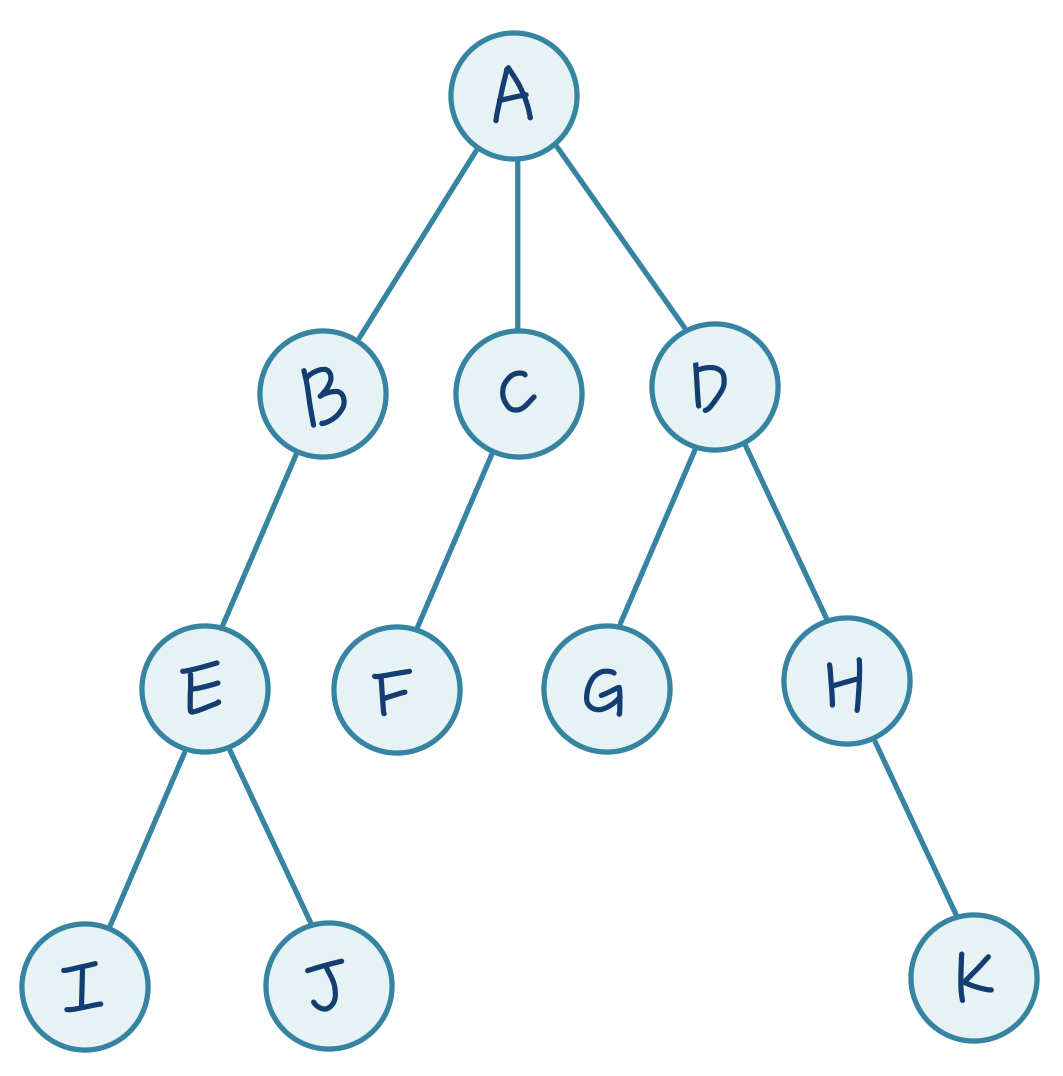
최대 깊이는 3, 총 노드 개수는 11개인 트리군요.
이제 이 트리를 가지고 두 탐색 알고리즘의 순서를 각각 비교하고, 과정을 모두 완벽하게 뜯어볼 겁니다. 한 번 뿌셔보시죠!
깊이 우선 탐색, Depth First Search (DFS)
깊이 우선 탐색, DFS는 위에서 "한 우물만 깊게 파서 끝을 보는 탐색" 이라고 얘기했었죠.
그렇다면 위의 간단한 트리에서 DFS 를 이용한다면 어떤 순서로 탐색을 하게 될까요?
먼저 루트 노드 (시작점) 인 A 부터 시작해서, 그 자식인 B, C, D 를 확인할 것입니다. 그 중 하나를 골라 더 깊게 들어가겠죠. B 를 골라서 들어간다면, 또 그 다음 자식인 E 로 내려가고, 그 후에 I 까지 확인하니 끝을 만납니다. 이런 식으로 모든 노드들의 끝을 볼 때까지 계속 깊게 들어가면서 탐색할 겁니다.
정확한 순서는, A → B → E → I → J → C → F → D → G → H → K 가 됩니다. 그림으로 보면 다음과 같죠!

이 순서가 어떻게 나오는지 스택까지 같이 보면서 확인해 보겠습니다.
아래 그림의 다홍색 박스가 스택입니다. 차곡차곡 노드들을 쌓아 넣고, 다시 꺼낼 때는 맨 위에 있는 노드, 즉 방금 넣은 노드부터 꺼내야 하죠.
DFS에서는 한 단계에서 Pop 과 Expand 두 가지 일을 동시에 처리합니다.
Pop은 스택의 맨 위 노드를 꺼내는 일을 말합니다. 그림에서는 / 를 이용해 노드를 지우는 것으로 표현합니다.Expand는 pop으로 노드를 지우면서 그 노드의 자식을 모두 스택에 넣는 일을 말합니다. 자식이 없다면 아무것도 넣지 않습니다.
따라서 위의 두 가지 일을 순서대로 처리하면 다음과 같이 13단계를 거쳐 모든 노드의 탐색을 할 수 있습니다.

그림을 손으로 직접 그리고 지워보면서 순서대로 따라가 보세요!
- 루트 노드 (시작점) 인
A를 스택에 넣습니다. A를Pop하면서Expand합니다. 즉,A는 지우고A의 자식인B,C,D를 스택에 넣습니다.- 스택의 맨 위에 있는
B를PopandExpand합니다. 즉,B는 지우고B의 자식인E를 스택에 넣습니다. - 스택의 맨 위에 있는
E를PopandExpand합니다. 즉,E는 지우고E의 자식인I,J를 스택에 넣습니다. - 스택의 맨 위에 있는
I를PopandExpand합니다. 이 때,I는 자식이 없으므로 (끝에 도달했으므로) 스택에 넣을 것이 없습니다. - 스택의 맨 위에 있는
J를PopandExpand합니다. 이 때,J또한 자식이 없으므로 스택에 넣을 것이 없습니다. - 스택의 맨 위에 있는
C를PopandExpand합니다. 즉,C는 지우고C의 자식인F를 스택에 넣습니다. - 스택의 맨 위에 있는
F를PopandExpand합니다. 이 때,F는 자식이 없으므로 스택에 넣을 것이 없습니다. - 스택의 맨 위에 있는
D를PopandExpand합니다. 즉,D는 지우고D의 자식인H,K를 스택에 넣습니다. - 스택의 맨 위에 있는
G를PopandExpand합니다. 이 때,G는 자식이 없으므로 스택에 넣을 것이 없습니다. - 스택의 맨 위에 있는
H를PopandExpand합니다. 이 때,H는 자식이 없으므로 스택에 넣을 것이 없습니다. - 스택의 맨 위에 있는
K를PopandExpand합니다. 이 때,K는 자식이 없으므로 스택에 넣을 것이 없습니다. - 스택이 비었습니다. 이 말은 모든 노드를 탐색했다는 뜻이죠!
이렇게 간단한 트리에서의 DFS 탐색 과정을 모두 알아보았습니다.
그렇다면 조금 더 복잡한 트리에서 DFS 탐색 순서는 어떻게 될지 한 번 풀어볼까요? 조금 더 복잡할 뿐, 원리는 같습니다!
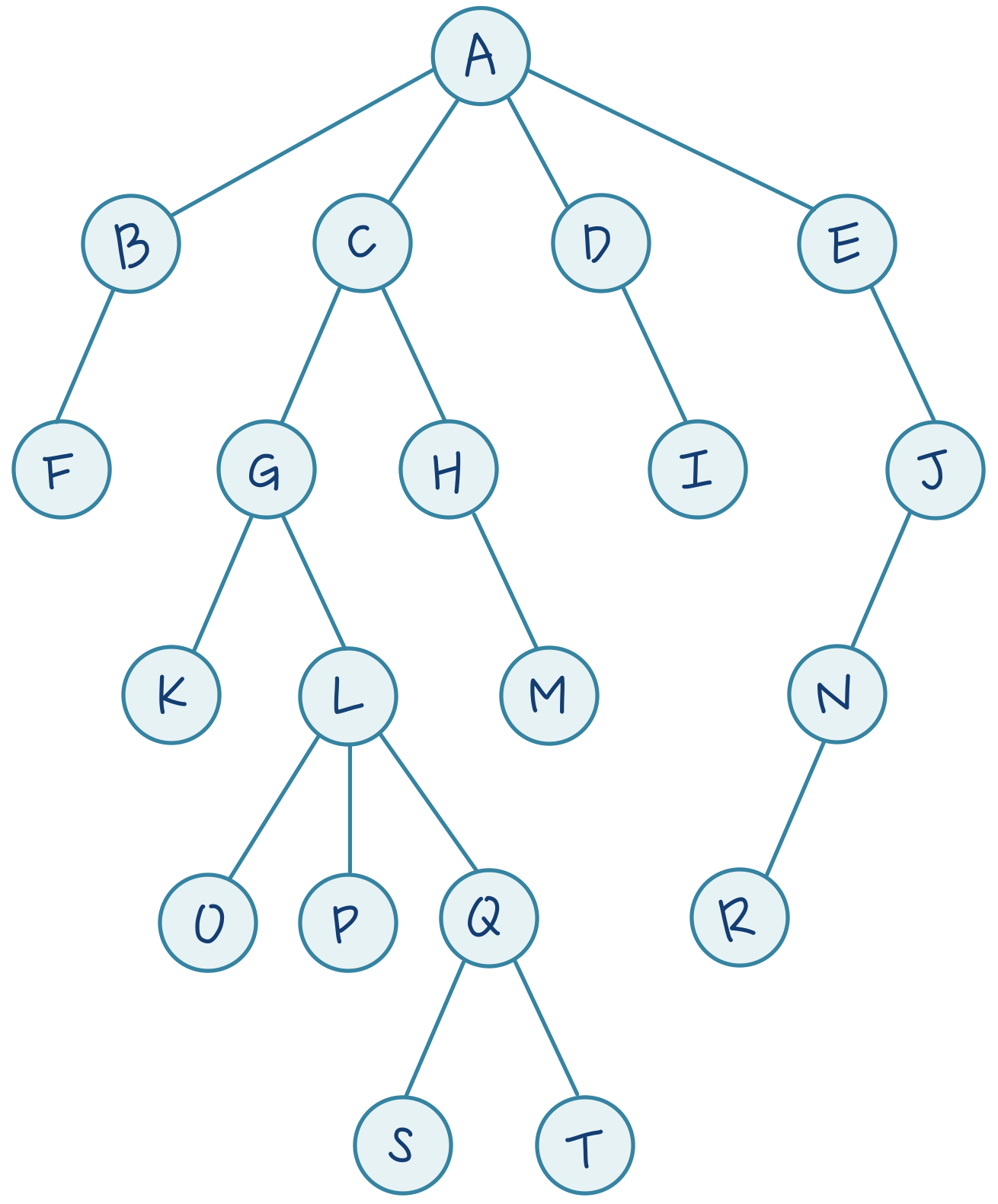
( 답을 보기 전에 한 번 탐색 경로를 찾아보세요! )
답은 A → B → F → C → G → K → L → O → P → Q → S → T → H →M→ D → I → E → J → N → R 입니다. 간단하죠?!
마지막으로, DFS 를 구현하는 파이썬 코드를 확인해 보겠습니다.
def DFS(start_node):
# 1) stack 에 첫 번째 노드 넣으면서 시작
stack = [start_node, ]
while True:
# 2) stack이 비어있는지 확인
if len(stack) == 0:
print('All node searched.')
return None
# 3) stack에서 맨 위의 노드를 pop
node = stack.pop()
# 4) 만약 node가 찾고자 하는 target이라면 서치 중단!
if node == TARGET:
print('The target found.')
return node
# 5) node의 자식을 expand 해서 children에 저장
children = expand(node)
# 6) children을 stack에 쌓기
stack.extend(children)
# 7) 이렇게 target을 찾거나, 전부 탐색해서 stack이 빌 때까지 while문 반복
괜찮은가요? 위에서 쭉 봐왔던 과정을 그대로 코드로 옮긴 것인데, 주석을 지우면 꽤 간단할 겁니다..!
- 처음 노드를 stack에 넣으면서 시작하고,
- while 문에 들어가면서 stack이 비었는지 확인합니다. 비어있다는 것은 모든 노드를 탐색했다는 뜻인데, 만약 찾고자 하는 TARGET 이 있는데 스택이 비었다면 "전부 찾아봤지만 TARGET 은 없었다"는 뜻이 되겠죠.
- 스택이 비어있지 않다면 맨 위에서 노드 하나를
pop합니다. - 방금 꺼낸 노드가 TARGET 인지 확인 해봐야겠죠! 일치한다면 원하는 타겟을 찾은 것입니다!
- 타겟이 아니라면 노드를
expand해서 자식 노드들을 구하고, - 그 자식 노드들을 stack 에 다시 차곡차곡 쌓습니다.
- 이렇게 target을 찾거나, 전부 탐색해서 stack이 빌 때까지 while 문을 반복하면 되겠습니다!
여기까지 DFS의 탐색 과정과 구현 코드까지 확인해 보았습니다. 다음은, DFS의 짝꿍인 BFS로 가시죠!
너비 우선 탐색, Breadth First Search (BFS)
너비 우선 탐색은 첫 번째 수에서 가능한 모든 것을 확인하고, 두 번째 수에서 가능한 모든 것을 확인하고, ... 이렇게 한 수 한 수 전부 확인하며 천천히 깊어지는 탐색이었습니다. 말로 하는 설명은 그만 하고, 바로 그림으로 확인해 보죠.
DFS 에서 사용했던 간단한 트리를 BFS 로 탐색하면 순서가 어떻게 달라질까요? 바로 다음 그림과 같습니다!
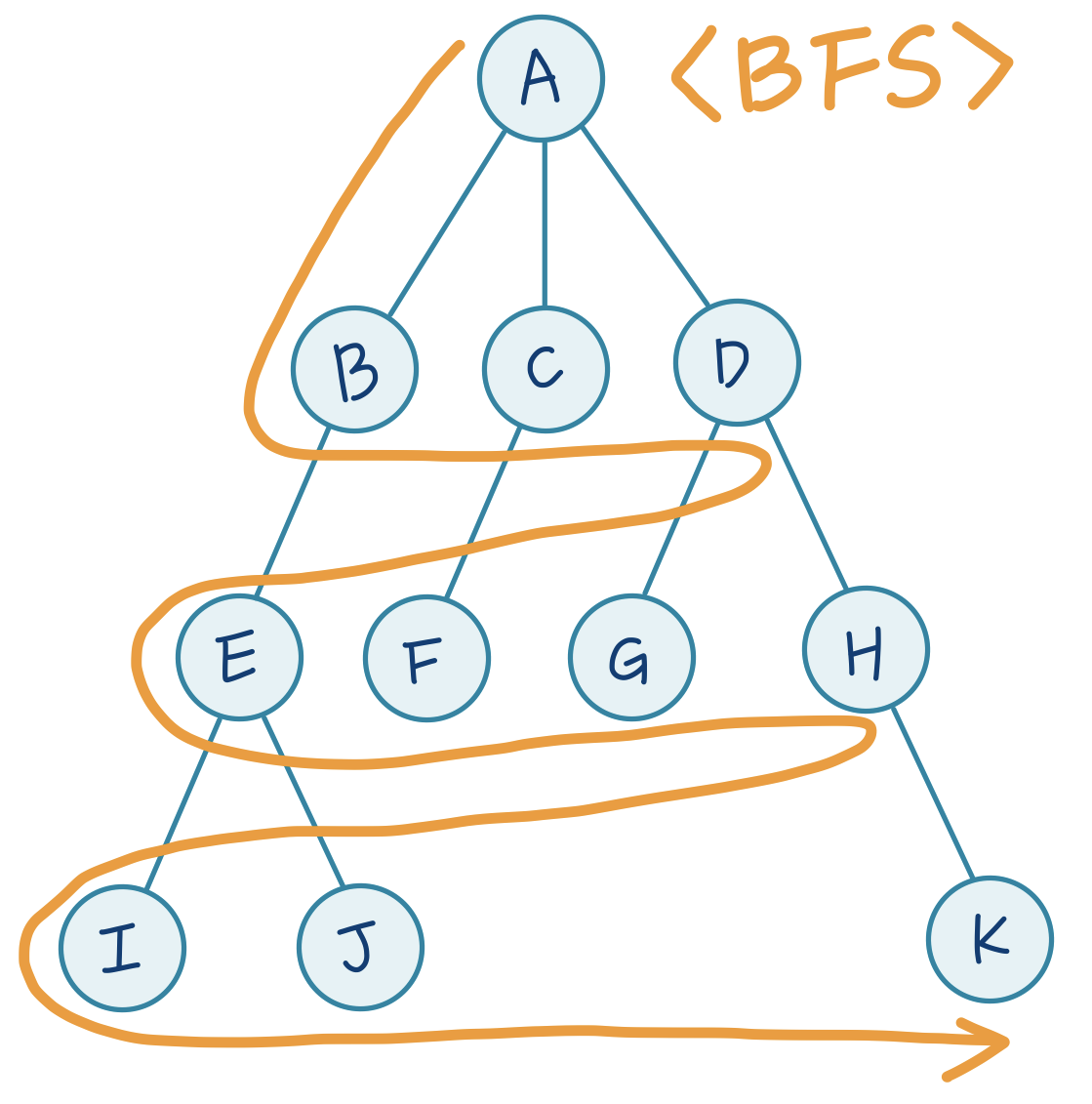
알파벳을 써 놓은 순서 그대로, A → B → C → D → E → F → G → H → I → J → K 가 되겠네요.
왜 이런 순서가 될까요?
말했듯이 BFS는 날개를 펼치듯 한 수에서 가능한 수를 다 그려보고, 그 다음 단계에서도 가능한 수를 다 확인하는 순서로 탐색하기 때문에 한 층을 내려가기 전에 그 층에 있는 모든 노드를 방문하기 때문입니다.
역시 BFS가 사용하는 자료구조 큐를 확인해 보면서 탐색 과정을 뜯어봅시다.
큐는 아래 그림에서 큐는 예시로 들었던 배드민턴 공을 담는 통처럼, 가로로 그려진 주황색의 열린 박스로 표현했고, 자료를 넣을 땐 오른쪽에서 넣고, 꺼낼 땐 왼쪽에서 꺼낼 것입니다.
BFS 또한 순서만 다를 뿐, Pop 과 Expand 과정을 똑같이 합니다. 다만, 스택의 pop 은 맨 뒤에서 꺼내지만 큐는 맨 앞에서 꺼내야 하기 때문에 용어가 조금 다릅니다. Pop 대신 Dequeue 라는 용어를 사용 하죠! (queue에 노드를 넣는 것은 Enqueue 라고 합니다. )
Dequeue는 큐에서 맨 앞에 있는 노드를 꺼내는 일입니다. 그림에서 / 를 이용해 표현했습니다.Expand는 dequeue로 노드를 지우면서 그 노드의 자식을 모두 큐에 넣는 일을 말합니다. 역시 자식이 없다면 아무것도 넣지 않습니다.
BFS의 과정도 위의 두 가지를 반복하면서 처리하면 다음과 같은 순서로 탐색하게 됩니다.

큐는 가장 왼쪽에 있는 노드만 꺼내기 때문에 노드가 지워지는 위치가 모두 같네요!
역시 그림 순서대로의 과정은 다음과 같습니다.
- 루트 노드 (시작점) 인
A를 큐에 넣습니다. A를Dequeue하면서Expand합니다. 즉,A는 지우고A의 바로 다음 자식인B,C,D를 큐의 오른쪽에 넣습니다.- 큐의 맨 왼쪽에 있는 B 를
DequeueandExpand합니다. 즉, B 는 지우고 B 의 바로 다음 자식인 E 만 큐에 넣습니다. - 큐의 맨 왼쪽에 있는
C를DequeueandExpand합니다. 즉,C는 지우고C의 바로 다음 자식인F를 큐에 넣습니다. - 큐의 맨 왼쪽에 있는
D를DequeueandExpand합니다. 즉,D는 지우고C의 바로 다음 자식인G,H를 큐에 넣습니다. - 큐의 맨 왼쪽에 있는
E를DequeueandExpand합니다. 즉,E는 지우고E의 바로 다음 자식인I,J를 큐에 넣습니다. - 큐의 맨 왼쪽에 있는
F를DequeueandExpand합니다. 이 때,F는 자식이 없으므로 큐에 넣을 것이 없습니다. - 큐의 맨 왼쪽에 있는
G를DequeueandExpand합니다. 이 때,G는 자식이 없으므로 큐에 넣을 것이 없습니다. - 큐의 맨 왼쪽에 있는
H를DequeueandExpand합니다. 즉,H는 지우고H의 바로 다음 자식인K를 큐에 넣습니다. - 큐의 맨 왼쪽에 있는
I를DequeueandExpand합니다. 이 때,I는 자식이 없으므로 큐에 넣을 것이 없습니다. - 큐의 맨 왼쪽에 있는
J를DequeueandExpand합니다. 이 때,J는 자식이 없으므로 큐에 넣을 것이 없습니다. - 큐의 맨 왼쪽에 있는
K를DequeueandExpand합니다. 이 때,K는 자식이 없으므로 큐에 넣을 것이 없습니다. - 큐가 비었습니다. 모든 노드를 탐색했다는 뜻이죠!
BFS 역시 탐색 과정을 완전히 이해했으니, 복잡한 트리도 간단히 해결 가능합니다. 순서는 어떻게 될까요?

( 답을 보기 전에 한 번 탐색 경로를 찾아보세요! )
이미 눈치 채셨겠지만, BFS는 알파벳을 써놓은 순서 그대로이네요.
A → B → C → D → E → F → G → H → I → J → K → L → M → N → O → P → Q → R → S → T 가 되겠습니다!
역시 파이썬 코드를 마지막으로 확인해 보겠습니다.
def BFS(start_node):
# 1) queue 에 첫 번째 노드 넣으면서 시작
queue = [start_node, ]
while True:
# 2) queue가 비어있는지 확인
if len(queue) == 0:
print('All node searched.')
return None
# 3) queue에서 맨 앞의 노드 를 dequeue (0번 인덱스를 pop)
node = queue.pop(0)
# 4) 만약 node가 찾고자 하는 target이라면 서치 중단!
if node == TARGET:
print('The target found.')
return node
# 5) node의 자식을 expand 해서 children에 저장
children = expand(node)
# 6) children을 stack에 쌓기
queue.extend(children)
# 7) 이렇게 target을 찾거나, 전부 탐색해서 queue가 빌 때까지 while문 반복
DFS와 아주 유사하죠!
다른 부분은 단지 다음 두 가지 뿐입니다.
1) queue를 이용한다는 것과 (사실 이것도 파이썬의 list로 같은 자료형을 사용하죠!),
2) pop 대신 dequeue를 한다는 것 (이 부분 또한 같은 pop 함수를 사용하지만, pop(0) 으로 0번 인덱스의 노드를 꺼내도록 했습니다.)
지금까지 탐색 알고리즘이 무엇인지, 어디에서 요긴하게 쓰이는지를 알아보고,
탐색 알고리즘에서 활용되는 자료구조인 스택과 큐를 알아보았습니다.
추가로 DFS 와 BFS 의 탐색 과정을 뜯어보고, 간단한 구현까지 마쳤네요!
DFS와 BFS는 아주 원초적인 알고리즘이라서,
마치 도서관에서 아무런 분류체계도 없이 책 하나하나를 일일이 다 찾아보는 것과 같다고 했습니다.
그렇다면 조금 더 좋은 알고리즘도 알아봐야겠죠.
다음 글에서 효율을 고려하며 탐색하는 A* 알고리즘에 대해 알아보면서,
8-puzzle과 미로찾기 예제에 DFS, BFS, A* 알고리즘을 모두 직접 적용시켜 구현하는 것을 확인해 보겠습니다.
그럼, 바로! → 다음 글 ← 로 가보시죠!!!
(는 아직 작성..중..)
References
- 그림 [이진트리, 무엇을 위한 걸까] : http://ycpcs.github.io/cs201-fall2015/lectures/binarySearchTrees.html
- 그림 [알파고가 검색하는 (아주 복잡한) 트리] : [Computing Space VIII] Games Cartographers Play: Alphago, Neural Networks and Tobler’s First Law
- 그림 [한국 십진분류표] : https://theuranus.tistory.com/4401
- 그림 [우리 모두 한 번쯤 해봤을 8-puzzle] : https://www.datasciencecentral.com/profiles/blogs/using-uninformed-informed-search-algorithms-to-solve-8-puzzle-n